ra2 studio - Fotolia
Machine learning : la différence entre une corrélation et une régression linéaire
En statistiques, en analytique et en machine learning, l’on utilise régulièrement des corrélations et des régressions linéaires. Cet article établit leur complémentarité et leurs différences.
Une corrélation est une opération pour déterminer s’il existe un lien statistique linéaire fort entre deux variables quantitatives à l’échelle relative (qui identifie les intervalles entre les données et où la position de zéro est définie arbitrairement, comme sur un thermomètre) ou à l’échelle absolue (soit une échelle relative où zéro a une position absolue : cela permet de quantifier la différence entre deux éléments, comme avec l’échelle de Kelvin).
La corrélation linéaire
L’une de ces variables est dite indépendante ou explicative. Souvent représentée par la lettre X, elle est dite indépendante, car elle n’est pas influencée par les autres paramètres d’un calcul. Ces variables sont généralement imposées par la nature : le temps, l’âge, le sexe, etc. La deuxième variable, est dite dépendante ou à expliquer. Elle est identifiée par la lettre Y. Sa valeur évolue suivant les changements de la variable indépendante.
La corrélation linéaire, ou corrélation de Pearson, vise donc à établir une mesure de l’association linéaire, ou la force d’un lien entre deux variables X et Y (sur un diagramme, X est placé en abscisse et Y en ordonnée). Cette mesure est nommée coefficient de corrélation, ou r dans un rapport de corrélation. R est une valeur sans unité comprise entre -1 et 1.
Une corrélation linéaire est positive quand les deux variables X et Y augmentent de concert. Par exemple, l’on peut essayer d’estimer une corrélation linéaire entre l’âge d’un groupe de personnes (un échantillon) et leurs revenus. Si r = 0,99, alors la corrélation linéaire entre ces deux variables est positive et forte. En clair, plus ces personnes sont âgées, plus elles bénéficient de rémunérations élevées. Si r = 0,01, la force de la corrélation est faible, mais toujours positive. Si r = -1, la corrélation est négative dans ce cas-là, les valeurs d’une variable augmentent quand celles de l’autre variable diminuent. Ici, cela voudrait dire que notre rapport entre l’âge et la richesse est infondé. Il est inexistant quand r = 0.
Les différentes sortes de corrélation.
La régression linéaire
La régression linéaire, très utilisée en data science, cherche aussi à établir une relation linéaire entre les variables X et Y en se basant sur la corrélation entre ces deux variables. Il s’agit d’une technique visant à prédire des valeurs futures, en utilisant le modèle suivant :
Y = a0 + a1 X1 +… + ak Xk + Error
Ici, Y est la réponse (ce que nous voulons prédire, par exemple le chiffre d’affaires), tandis que les Xi sont les prédicteurs (par exemple le sexe, avec 0 = homme, 1 = femme, le niveau d’éducation, l’âge, etc.)
En général, les prédicteurs sont quelque peu corrélés à la réponse. Dans la régression, nous voulons maximiser la valeur absolue de la corrélation entre la réponse observée et la combinaison linéaire des prédicteurs. Nous choisissons les paramètres a0,…, ak qui permettent d’atteindre cet objectif.
La régression linéaire est généralement représentée par une droite traversant un nuage de points figurant sur un diagramme. En clair, cette droite doit se rapprocher le plus possible de ces points, c’est-à-dire que l’on souhaite minimiser les écarts précédents. La simple observation d’une telle visualisation permet de déterminer la pertinence d’une régression linéaire simple.
En probabilité et en statistiques, la méthode des moindres carrés est justement utilisée pour minimaliser la somme des carrés des écarts entre chaque point du nuage.
Le carré du coefficient de corrélation en question est appelé coefficient R-carré. Les coefficients a0,…, ak sont appelés les paramètres du modèle et a0 (parfois fixé à zéro) est appelé l’interception.
Le coefficient R-carré est un coefficient de détermination, il permet de juger de la qualité de la régression linéaire simple, c’est-à-dire si la droite de régression a un pouvoir de prédiction nul, faible ou fort. La valeur du coefficient varie entre 0 et 1. Quand R-carré vaut 1, alors la régression linéaire peut déterminer 100 % de la distribution des points. En machine learning et plus particulièrement en apprentissage supervisé, ce calcul de l’erreur entre la valeur prédite et la valeur véritable revient à rechercher la fonction coût.
Or la méthode des moindres carrés s’avère consommatrice en ressources computationnelles avec de gros volumes de données, car il faut calculer l’écart type entre chaque point de la distribution. Certains data scientists lui privilégient la méthode de descente de gradient, un algorithme d’optimisation différentiable s’appliquant de manière itérative pour trouver le minimum de la fonction. D’autres lui préfèrent la décomposition en valeurs singulières (en anglais, singular value decomposition ou SVD) pour résoudre le problème des moindres carrés, souvent combinée à la notion de pseudo-inverse de Moore Penrose pour la rendre plus stable et plus fiable. Cet emploi de la SVD n’est pas forcément moins coûteux, mais plus rapide.
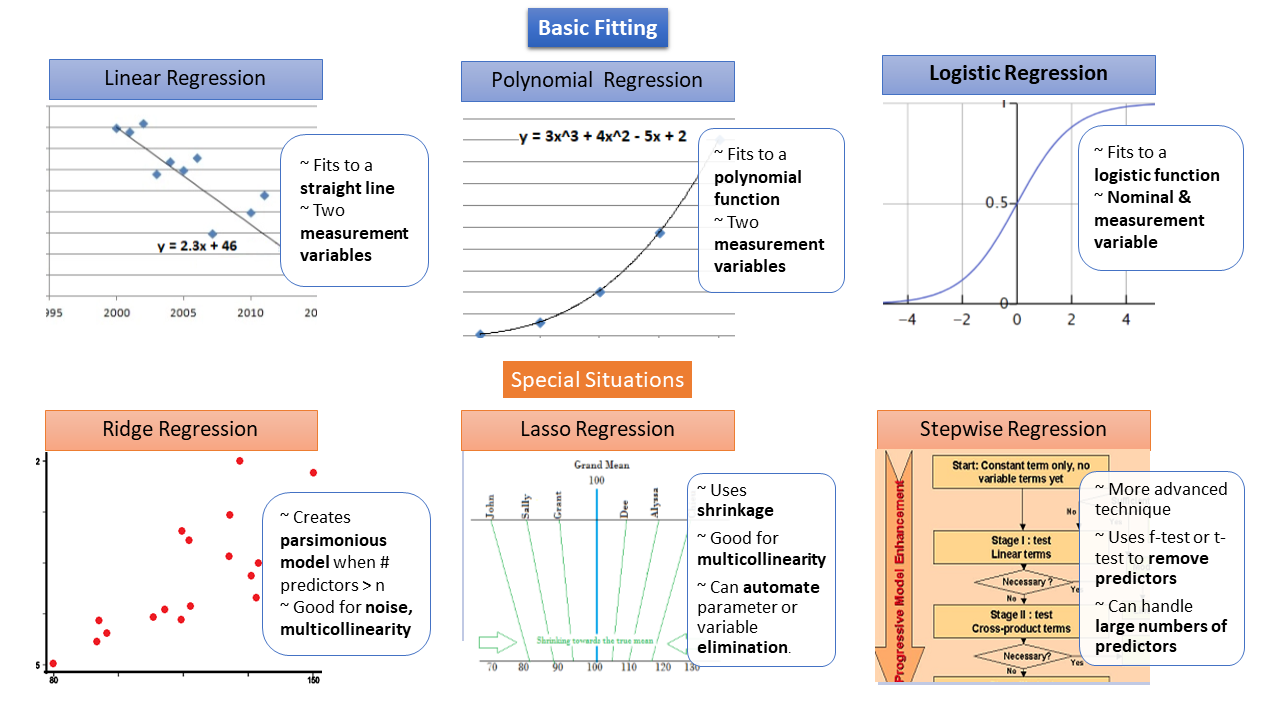Les différents types de régression.
Il existe plusieurs types de corrélation et de régression accessibles suivant le problème que l’on cherche à résoudre. Les deux illustrations figurant dans cet article résument les options disponibles et leurs usages.
Cet article est originellement paru dans les colonnes de DataScienceCentral.com, propriété de Techtarget, également propriétaire du MagIT.
Vincent Granville est un data scientist, cofondateur et directeur associé de DataScienceCentral.com. Vincent est également l’auteur de plusieurs eBooks plubliés sur ce site et sur DataShaping.com
