Le clustering k-means expliqué avec des exemples

Quand utiliser l’algorithme de clustering k-means ?

Le partitionnement en K-moyennes s’appuie sur un algorithme relativement rapide qui convient aux grands ensembles de données.

Exemple ? Le regroupement des valeurs RVB. Les données se présentent sous la forme suivante : R, G et B représentent l’intensité du rouge, du vert et du bleu d’une seule couleur. Il existe 16 millions de combinaisons RVB différentes, mais vous pouvez utiliser l’algorithme des k-moyennes pour réduire un ensemble de valeurs RVB à un plus petit nombre. Par exemple, si vous choisissez une valeur k de 256, 256 groupes de couleurs similaires seront créés. Vous pouvez faire correspondre les 256 groupes à une seule couleur. Vous pouvez ensuite réduire l’ensemble à seulement 256 couleurs.

Le défi de l’algorithme de regroupement des k-moyennes

L’algorithme K-means ne peut pas traiter les attributs catégoriels, car il n’y a aucun moyen d’incorporer les données non numériques.

La méthode est néanmoins intéressante pour rapprocher des phrases ou des mots de sens similaires. C’est pourquoi en NLP ou dans le domaine plus spécifique de l’IA générative, les données textuelles et audiovisuelles sont vectorisées, c’est-à-dire représentées sous forme de séquences de chiffres, souvent allant de -1 à 1.

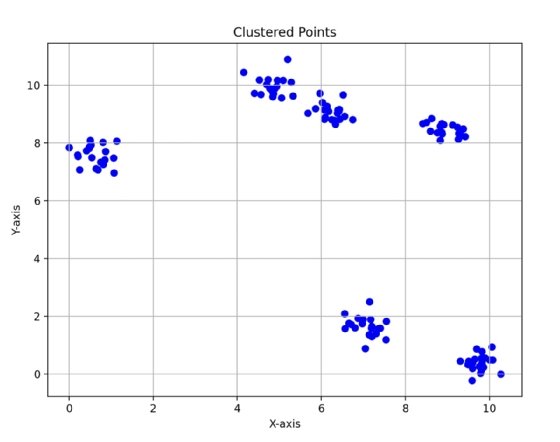
En outre, les données qui contiennent des grappes de forme irrégulière lui siéent mal. Avec l’illustration 1, vous pouvez voir qu’il existe des grappes circulaires distinctes dans les données. Le regroupement par K-means est bien adapté aux données qui sont regroupées en formes sphériques – du fait du calcul par l’algorithme d’un centroïde qui est la moyenne de tous les points de chaque groupe –, ou qui peuvent être séparées par une ligne droite. Cela veut aussi dire que les clusters en forme de lune ou de spirale ne sont pas correctement identifiés.

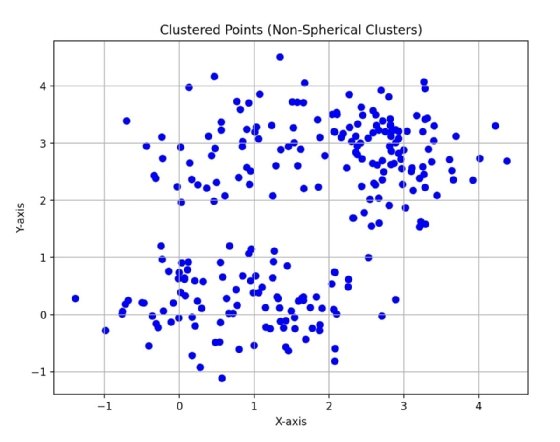
L’illustration 2 montre deux grappes, mais les points de données ne sont pas aussi étroitement regroupés que dans l’illustration 1, et ils ne sont pas tout à fait sphériques. Il est plus difficile pour l’algorithme de percevoir la séparation pourtant visible à l’œil nu pour un humain, puisque le regroupement des données n’est pas sphérique.

Utiliser la méthode du coude pour choisir la valeur k

Il est important de choisir la bonne valeur de k pour réussir à appliquer l’algorithme des k-moyennes. Si la valeur de k est trop petite, les grappes contiendront des points qui seraient mieux placés dans des grappes distinctes. Si la valeur de k est trop grande, les grappes seront divisées inutilement. Cela conduit à des grappes distinctes qui sont mieux représentées sous la forme d’une seule grappe.

Pour choisir une valeur de k à l’aide de la méthode du coude, vous devez exécuter l’algorithme k-means plusieurs fois avec différentes valeurs de k.

Après avoir exécuté l’algorithme sur les données avec une valeur de k comprise entre 1 et 10, calculez une valeur qui vous indique la densité de la grappe pour chaque exécution. La somme des distances au carré, entre chaque point et le centroïde de la grappe qui lui a été attribué, sera calculée et vous donnera une représentation du degré de regroupement des grappes. C’est ce que l’on appelle communément la somme des carrés à l’intérieur des grappes (WCSS). Cette valeur est rapportée à la valeur k, ce qui donne un graphique semblable à celui de l’illustration 3.

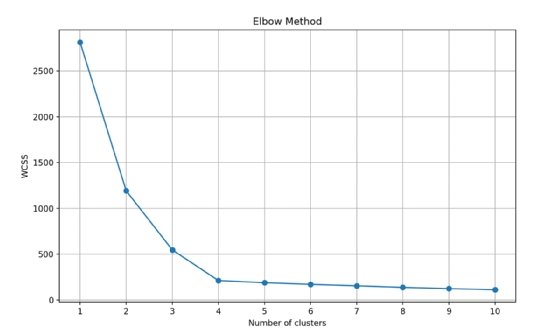
Imaginez que les valeurs tracées représentent un bras et que le point où les valeurs changent brusquement est le coude. La valeur k idéale est celle où la valeur WCSS commence à se stabiliser par rapport au nombre de grappes. Dans le cas de l’illustration 3, une valeur k de 4 ou 5 serait idéale.

Utiliser la méthode de la silhouette pour choisir la valeur k

La méthode de la silhouette permet de déterminer le nombre de grappes dans lesquelles les points de données sont les mieux placés et sont bien séparés des autres grappes.

Pour chaque point de données, mesurez la distance moyenne entre le point de données et les autres points de la même grappe. Cela représente le degré d’intégration du point de données dans sa propre grappe. Appelons cette valeur b.

Pour chaque point de données, calculez la plus petite distance moyenne entre le point de données et les points d’un autre groupe. Cette valeur représente le degré de distinction du point de données par rapport aux autres groupes. Nous appellerons cette valeur c.

Introduisez les deux valeurs dans la formule suivante :

s = (c − b) ÷ max(b, c)

Cette formule permet d’obtenir un score de silhouette. Cela vous permet d’évaluer chaque point en vue d’un regroupement optimal.

Si b est beaucoup plus petit que c, le point est bien regroupé et obtient un score proche de 1. Si b et c sont similaires, le point est à la frontière de deux groupes et obtient un score proche de 0. Si b est beaucoup plus grand que c, le point peut se trouver dans le mauvais groupe et obtient un score proche de -1.

Pour avoir une idée de la précision des résultats globaux du regroupement, faites la moyenne des scores de silhouette de tous les points de données pour chaque valeur de k. La valeur optimale de k est celle qui donne le score de silhouette moyen le plus élevé. Celui-ci vous indique le nombre de grappes, ou la valeur de k qui donne le meilleur ajustement global pour les données.

Démonstration du K-means Clustering avec Python

Vous pouvez mettre en œuvre l’algorithme des k-moyennes en Python. Tout d’abord, vous devrez définir une fonction pour calculer la distance euclidienne, puis créer des données aléatoires.

# Function to calculate Euclidean distance
def euclidean_distance(x1, x2):
   return np.sqrt(np.sum((x1 - x2) ** 2))

# Generate sample data
X = np.random.randn(300, 2)

Ensuite, créez une classe KMeans. Elle contiendra l’implémentation de l’algorithme k-means.

# KMeans class
class KMeans:
   def __init__(self, k=3, max_iters=100):
       self.k = k
       self.max_iters = max_iters

La méthode __init__ définit la valeur k à utiliser, ainsi que la valeur max_iters qui est fixée par défaut à 100. Cette valeur par défaut est importante pour limiter le nombre maximal d’exécutions de l’algorithme.

# Initialize centroids as randomly selected data points
def initialize_centroids(self, X):
   centroids_idx = np.random.choice(X.shape[0], self.k, replace=False)
   return X[centroids_idx]

Vous avez besoin d’une fonction permettant à l’algorithme de sélectionner aléatoirement les centroïdes des grappes. La fonction initialize_centroids prend un ensemble de points de données et choisit aléatoirement k points comme centroïdes à utiliser pour le regroupement.

Une fois que les centroïdes aléatoires ont été sélectionnés, vous pouvez affecter les points aux grappes à l’aide de la méthode assign_clusters. Celle-ci prend les points de données et les centroïdes comme arguments.

# Assign each data point to the nearest centroid
def assign_clusters(self, X, centroids):
   clusters = [[] for _ in range(self.k)]
   for i, x in enumerate(X):
       distances = [euclidean_distance(x, centroid) for centroid in centroids]
       cluster_idx = np.argmin(distances)
       clusters[cluster_idx].append(i)
   return clusters

Pour affecter un point de données à une grappe, calculez la distance euclidienne entre le point et chacun des centroïdes. Le point de données est affecté à la grappe dont le centroïde a la plus petite distance euclidienne par rapport au point de données.

Une fois que tous les points de données ont été affectés aux grappes, les centroïdes sont mis à jour en fonction de la moyenne de tous les points affectés à la grappe. Ensuite, la méthode update_centroids prend les points de données et les grappes comme arguments, itère sur les grappes pour calculer la valeur moyenne – le véritable centre de la grappe – et renvoie ces valeurs en tant que centroïdes de chaque grappe.

# Update centroids by taking the mean of all points assigned to the centroid
def update_centroids(self, X, clusters):
   centroids = np.zeros((self.k, X.shape[1]))
   for i, cluster in enumerate(clusters):
       cluster_mean = np.mean(X[cluster], axis=0)
       centroids[i] = cluster_mean
   return centroids

Ensuite, vérifiez si les vrais centroïdes sont similaires aux centroïdes attribués aléatoirement au début de l’exécution de l’algorithme. Si c’est le cas, les grappes ont été correctement créées et contiennent des points de données proches de leurs centroïdes.

Dans le cas inverse, recommencez l’ensemble du processus et revenez au point de départ où vous avez attribué des points de données aléatoires comme centroïdes.

Voici à quoi ressemble la méthode fit de notre classe KMeans, qui utilise les autres méthodes que vous avez utilisées.

def fit(self, X):
   self.centroids = self.initialize_centroids(X)
   for _ in range(self.max_iters):
       clusters = self.assign_clusters(X, self.centroids)
       prev_centroids = self.centroids
       self.centroids = self.update_centroids(X, clusters)
       # If centroids don't change much, break
       if np.allclose(prev_centroids, self.centroids):
           break